Resolver numericamente os problemas abaixo.
1. Ana decidiu, com pesar, que precisa vender seu carro, um Chevrolet Celta 1.0 4P (ex), modelo 2011, com 63.000km rodados. Seu colega, Carlos fez uma proposta. Ana, que não acompanha a dinâmica do mercado automotivo, não faz ideia se a proposta de Carlos é justa. Mas Ana resolve descobrir o valor de mercado de seu estimado carro. O roteiro que Ana seguiu foi o seguinte:
(a) Pesquisou em um site de anúncios de carros usados, por ofertas de carros do mesmo modelo, com no máximo 10 anos de uso, em sua região.
(b) Montou uma tabela com ano do modelo, a quilometragem e o preço anunciado dos carros. Para ter confiança na estimativa que faria, coletou informação de pelo menos de 40 anúncios, tomando o cuidado de ter pelo menos 3 anúncios de carros de cada ano pesquisado.
(c) Utilizando seus conhecimentos numéricos, descobriu os coeficientes c0; c1 e c2 da função P = c0 + c1A + c2K; onde P é o preço anunciado do carro, A representa o ano do modelo e K a quilometragem do carro, sendo que todas as quantidades foram normalizadas e adimensionalizadas.
Com base nessa análise, Ana estimou o valor de mercado de seu veículo. O que sabemos é que Carlos e Ana fecharam o negócio, e todos ficaram felizes. Siga o roteiro de Ana e estime o valor de mercado do veículo dela.
Carro
|
PREÇO (RS)
|
QUILOMETRAGEM (Km)
|
ANO
|
1
|
17.980
|
82.000
|
2006
|
2
|
14.900
|
106.000
|
2006
|
3
|
19.000
|
117.000
|
2006
|
4
|
15.800
|
156.763
|
2007
|
5
|
14.590
|
100
|
2007
|
6
|
15.500
|
75.000
|
2007
|
7
|
13.900
|
116.000
|
2007
|
8
|
15.500
|
111.000
|
2008
|
9
|
16.900
|
113.000
|
2008
|
10
|
16.500
|
108.000
|
2008
|
11
|
11.000
|
68.000
|
2008
|
12
|
11.990
|
153.671
|
2008
|
13
|
15.890
|
108.752
|
2009
|
14
|
17.990
|
90.000
|
2009
|
15
|
17.990
|
39.715
|
2009
|
16
|
15.890
|
108.752
|
2009
|
17
|
14.990
|
99.700
|
2010
|
18
|
13.899
|
89.000
|
2010
|
19
|
21.900
|
100
|
2010
|
20
|
16.900
|
75.800
|
2011
|
21
|
16.500
|
90657
|
2011
|
22
|
19.500
|
70.000
|
2011
|
23
|
23.990
|
90.553
|
2012
|
24
|
23.990
|
83.002
|
2012
|
25
|
23.990
|
62.640
|
2012
|
26
|
23.990
|
37.000
|
2012
|
27
|
24.900
|
48.500
|
2012
|
28
|
22.900
|
52.099
|
2012
|
29
|
26.890
|
46.070
|
2012
|
30
|
25.900
|
35.350
|
2012
|
31
|
23.500
|
46.000
|
2012
|
32
|
27.800
|
22.000
|
2013
|
33
|
23.990
|
74.356
|
2013
|
34
|
24.990
|
76.279
|
2013
|
35
|
28.900
|
28.000
|
2014
|
36
|
29.900
|
58.683
|
2014
|
37
|
27.900
|
42.036
|
2014
|
38
|
28.900
|
20.490
|
2015
|
39
|
31.900
|
111.111
|
2015
|
40
|
30.990
|
39.469
|
2015
|
Pi
|
Ki
|
ai
|
0,184604067
|
0,01266285
|
0,058333333
|
0,203742823
|
0,107496984
|
0,058333333
|
0,275991627
|
0,165219612
|
0,052777778
|
0,328192584
|
0,096920141
|
0,052777778
|
0,054630383
|
0,470539949
|
0,052777778
|
0,232929426
|
0,222999687
|
0,163888889
|
0,132450957
|
0,103303269
|
0,163888889
|
0,132450957
|
0,217672329
|
0,163888889
|
0,251589713
|
0,237348959
|
-0,275
|
0,184604067
|
0,250115215
|
-0,275
|
0,203742823
|
0,218199575
|
-0,275
|
0,237235646
|
0,529460051
|
0,386111111
|
0,295130383
|
0,470539949
|
0,386111111
|
0,251589713
|
0,007556347
|
0,386111111
|
0,132929426
|
0,052238244
|
0,497222222
|
0,280297847
|
0,205433319
|
0,497222222
|
0,084125598
|
0,275647728
|
0,497222222
|
0,060202153
|
0,024359294
|
0,058333333
|
0,389558612
|
0,340387967
|
0,502777778
|
0,533099282
|
0,238057486
|
0,502777778
|
0,489558612
|
0,219242578
|
0,502777778
|
0,389558612
|
0,292450674
|
0,391666667
|
0,437405502
|
0,096597154
|
0,391666667
|
0,341711722
|
0,202857088
|
0,391666667
|
0,336927033
|
0,330749443
|
0,280555556
|
0,154630383
|
0,003445613
|
0,280555556
|
0,202477273
|
0,015720368
|
0,280555556
|
0,154630383
|
0,106833139
|
0,169444444
|
0,154630383
|
0,058634138
|
0,169444444
|
0,154630383
|
0,071339116
|
0,169444444
|
0,154630383
|
0,235002521
|
0,169444444
|
0,198171053
|
0,161596548
|
0,169444444
|
0,102477273
|
-0,13862367
|
0,169444444
|
0,293386364
|
0,177107549
|
0,169444444
|
0,246017943
|
0,245534683
|
0,169444444
|
0,131185407
|
0,177554368
|
0,169444444
|
0,336927033
|
0,330749443
|
0,280555556
|
0,154630383
|
0,003445613
|
0,280555556
|
0,202477273
|
0,015720368
|
0,280555556
|
0,389558612
|
0,292450674
|
0,391666667
|
Utilizando da equação de métodos de mínimos quadrados com matrizes:
Realizando a operação temos:
M = 40 80419 2952648 80419 161680677 5934231346 2952648 5934231346 273440019650
Para N =
Temos:
N = 18732,75744 -9,30524 -0,00034 -9,3052413 0,004622282 1,66079E-7 -0,000335668 1,66079E-7 2,39895E-11
Multiplicando as matrizes M e N: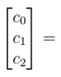
-3456779,292 1730,40993 -0,019029961
Portanto a equação de Ana terá os seguintes coeficientes:
P = c0 + c1A + c2K → P = -3456779,292 + 1730,40993A - 0,01902996K (1)
O erro médio quadrático é dado pela equação:
Onde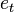 
= Preço anunciado – Preço de previsão.
= Preço anunciado – Preço de previsão.
Observação: A previsão de mercado foi obtida substituindo os valores de A e K na equação (1).
Previsão de Mercado
|
Preço anunciado
|
Diferença²
|
R$ 12.862,57
|
R$ 17.980,00
|
26188081
|
R$ 12.405,85
|
R$ 14.900,00
|
6220775,14
|
R$ 12.196,52
|
R$ 19.000,00
|
46287309,4
|
R$ 13.170,24
|
R$ 15.800,00
|
6915617,2
|
R$ 16.151,53
|
R$ 14.590,00
|
2438390,04
|
R$ 14.726,19
|
R$ 15.500,00
|
598781,127
|
R$ 13.945,96
|
R$ 13.900,00
|
2112,51923
|
R$ 15.771,52
|
R$ 15.500,00
|
73724,1313
|
R$ 15.733,46
|
R$ 16.900,00
|
1360811
|
R$ 15.828,61
|
R$ 16.500,00
|
450762,169
|
R$ 16.589,81
|
R$ 11.000,00
|
31245977,6
|
R$ 14.959,49
|
R$ 11.990,00
|
8817897,33
|
R$ 17.544,71
|
R$ 15.890,00
|
2738069,02
|
R$ 17.901,56
|
R$ 17.990,00
|
7821,46203
|
R$ 18.858,48
|
R$ 17.990,00
|
754261,868
|
R$ 17.544,71
|
R$ 15.890,00
|
2738069,02
|
R$ 19.447,38
|
R$ 14.990,00
|
19868239
|
R$ 19.651,00
|
R$ 13.899,00
|
33085513,9
|
R$ 21.342,76
|
R$ 21.900,00
|
310511,621
|
R$ 21.632,61
|
R$ 16.900,00
|
22397562
|
R$ 21.349,88
|
R$ 16.500,00
|
23521318
|
R$ 21.742,98
|
R$ 19.500,00
|
5030959,41
|
R$ 23.082,27
|
R$ 23.990,00
|
823978,851
|
R$ 23.225,96
|
R$ 23.990,00
|
583753,424
|
R$ 23.613,45
|
R$ 23.990,00
|
141789,552
|
R$ 24.101,38
|
R$ 23.990,00
|
12405,2014
|
R$ 23.882,53
|
R$ 24.900,00
|
1035236,86
|
R$ 23.814,05
|
R$ 22.900,00
|
835478,763
|
R$ 23.928,78
|
R$ 26.890,00
|
8768842,23
|
R$ 24.132,78
|
R$ 25.900,00
|
3123073,34
|
R$ 23.930,11
|
R$ 23.500,00
|
184993,752
|
R$ 26.117,24
|
R$ 27.800,00
|
2831688,05
|
R$ 25.120,91
|
R$ 23.990,00
|
1278946,99
|
R$ 25.084,31
|
R$ 24.990,00
|
8894,52156
|
R$ 27.733,47
|
R$ 28.900,00
|
1360796,58
|
R$ 27.149,57
|
R$ 29.900,00
|
7564854,86
|
R$ 27.466,36
|
R$ 27.900,00
|
188040,509
|
R$ 29.606,79
|
R$ 28.900,00
|
499556,443
|
R$ 27.882,28
|
R$ 31.900,00
|
16142081,5
|
R$ 29.245,62
|
R$ 30.990,00
|
3042849,52
|
EQM = 7236996.
O EQM fornece um meio de escolher o melhor estimador: um EQM mínimo frequentemente indica a variação mínima e é, portanto, um bom estimador. Ter um Erro Quadrático Médio de zero é o ideal, mas na maioria das situações nunca é possível. Como o valor obtido é alto, concluímos que a função de Ana não é muito favorável.
Usando os critérios:
|hi| < 10% → Justo;
|hi| > 10% → Preço acima;
|hi| < 3% → Boa Oportunidade
|hi|
|
Avaliação
|
39,78543
|
RUIM
|
20,10461
|
RUIM
|
55,78211
|
RUIM
|
19,96741
|
RUIM
|
9,668026
|
JUSTO
|
5,254648
|
JUSTO
|
0,329573
|
MELHOR OPORTUNIDADE
|
1,721596
|
BOA OPORTUNIDADE
|
7,414376
|
JUSTO
|
4,241612
|
JUSTO
|
33,69424
|
RUIM
|
19,85023
|
RUIM
|
9,431396
|
JUSTO
|
0,49403
|
BOA OPORTUNIDADE
|
4,605262
|
JUSTO
|
9,431396
|
JUSTO
|
22,92021
|
RUIM
|
29,27078
|
RUIM
|
2,610888
|
BOA OPORTUNIDADE
|
21,87719
|
RUIM
|
22,71619
|
RUIM
|
10,31588
|
RUIM
|
3,932598
|
JUSTO
|
3,289584
|
JUSTO
|
1,59464
|
BOA OPORTUNIDADE
|
0,462126
|
BOA OPORTUNIDADE
|
4,260293
|
JUSTO
|
3,838261
|
JUSTO
|
12,37515
|
RUIM
|
7,322911
|
JUSTO
|
1,797355
|
BOA OPORTUNIDADE
|
6,443109
|
JUSTO
|
4,50185
|
JUSTO
|
0,375975
|
BOA OPORTUNIDADE
|
4,206224
|
JUSTO
|
10,13065
|
RUIM
|
1,578791
|
BOA OPORTUNIDADE
|
2,387267
|
BOA OPORTUNIDADE
|
14,40959
|
RUIM
|
5,964573
|
JUSTO
|
Analisando o coeficiente c2 da função, podemos chegar no valor de depreciação do preço do carro a cada 10.000km.
c2 = - 0,01902996
D = c2 * 10.000
D = -190,2996
O carro irá desvalorizar R$190,30 a cada 10.000km.
Analisando o coeficiente c1 da função, podemos chegar no valor de depreciação do preço do carro a cada ano.
c1 = 1730,40993
D = c1 * 1
D = 1730,41
O carro irá desvalorizar R$1.730,41 a cada ano a mais do ano de fabricação.
O valor justo para o Celta da Ana será:
P = -3456779,292 + (1730,40993*2011) - (0,01902996*63000)
P = 24273,96 → R$24.273,96
Nenhum comentário:
Postar um comentário