Cálculo Numérico : Lista 3A. Exercícios, resoluções e discussões.

Resolver analítica ou numericamente os problemas abaixo.

1. Descreva, fazendo um passo-a-passo explicativo (pode conter um pseudocódigo, fluxograma, etc), como resolver sistemas de equações lineares usando os métodos diretos: (i) de Cramer, (ii) eliminação de Gauss e (iii) decomposição A = LU.

Método de Cramer:

Consideramos o sistema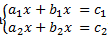

. Suponhamos, sem perda de generalidade, que a1≠0. Escalonando esse sistema (substituímos a 2ª equação pela soma dela com a 1ª multiplicando por –a2a1), temos

Lembremos que a matriz incompleta dos coeficientes do sistema é M=(a1 b1a2 b2). Assim, a1b2 - a2b1 é exatamente det M, que indicamos por D.

Se substituirmos, em M, a coluna dos coeficientes de y pela coluna dos coeficientes independes, obteremos (a1 c1a2 c2), cujo determinante é igual a a1c2 - a2c1, indicado por Dy.

Dessa forma na 2ª equação de (*) temos:

(a1b2 - a2b1)y=a1c2 - a2c1 ➔ D = Dy.

Se D ≠ 0, vem que y=-Dy D.

Substituindo y na 1ª equação (*), segue que:

(a1b2 - a2b1) . x=c1b2 - b1c2 (**)

Se substituirmos, em M, a coluna dos coeficientes de pela coluna dos coeficientes independentes, obteremos (c1 b1c2 b2), cujo determinante é c1b2 - b1c2, indicado por Dx.

Assim (**) temos:

D . x = Dy x=-DxD

Em resumo, o sistema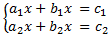

é possível e determinado se, e somente se,

M =|a1 b1a2 b2| ≠ 0. A solução do sistema é dada por:

x=-DxD e y=-Dy D

Os resultados acima são conhecidos como Regra de Cramer e podem ser generalizados para um sistema n x m (n equações e n incógnitas). A Regra de Cramer é um importante recurso da resolução de sistemas lineares possíveis e determinados, especialmente quando o escalonamento se torna muito trabalhoso (por causa dos coeficientes das equações do sistema), ou ainda quando o sistema é literal.

Fonte: IEZZI, G.; DOLCE, O.; DEGENSZAJN, D. M; PÉRIGO, R. Matemática volume único. São Paulo: Atual Editora, Cap. 22 p. 397 - 398.

Método de Eliminação de Gauss

O método da Eliminação de Gauss consiste em transformar o sistema linear original num sistema linear equivalente com a matriz dos coeficientes triangular superior, pois estes são de resolução imediata. Dizemos que dois sistemas lineares são equivalentes quando possuem a mesma solução.

Resolução de sistemas triangulares

Seja o sistema linear Ax = b, onde A: matriz n x n, triangular superior, com elementos da diagonal diferentes de zero. Escrevendo a equação desse sistema temos:

Da ultima equação temos

xn=bnann

xn-1 pode então ser obtido da penúltima equação:

xn-1 =bn-1-an-1, nxnan-1,n-1

E assim sucessivamente obtêm-se xn-2, ..., x2 e finalmente x1:

x1 =b1-a12x2 - a13x3 -… a1nxn a11

Descrição do método da Eliminação de Guass

TEOREMA 1

Seja Ax = b um sistema linear. Aplicando a este sistema uma sequencia de equações elementares escolhidas entre:

trocar duas equações;
multiplicar uma equação por uma constante não nula;
adicionar um múltiplo de uma equação a uma outra equação;

obtemos um novo um novo sistema Ax= b e os sistemas Ax = b e Ax= b são equivalentes.

Descrevemos a seguir como método de Eliminação de Gauss usa o teorema para triangularizar a matriz A. Vamos supor que det(A) ≠ 0.

A eliminação é efetuada por colunas que chamaremos etapa k do processo a fase em que se elimina a variável xk das equações k + 1, k + 2, ..., n.

Usaremos a notação aij (k) para denotar o coeficiente da linha i coluna j no final da k-ésima etapa, bem como bi (k) será o i-ésimo elemento do vetor constante na etapa k.

Considerando det(A) ≠ 0, é sempre possível reescreve o sistema linear de forma que o elemento da posição a11 seja diferente de zero, usando apenas a operação elementar (i):

Onde aij (0)=aij, bi (0) =bi e aij (0)≠ 0.

Exemplo:

Etapa 1

Etapa 2

Etapa 3

O algorítmico acima efetua, na fase da eliminação, 4n3+3n2-7n6, operações e para resolver o sistema triangular superior, o número de operações a estudar é n2.

Assim, o total de operações para se resolver um sistema linear pelo método da Eliminação de Gauss é 4n3+9n2-7n6.

Escalonamento sem pivoteamento

• Repetir da primeira até a penúltima coluna;

• Repetir para as linhas abaixo da diagonal principal;

• Aplicar operação elementar com o objetivo de zerar o elemento da linha corrente abaixo da diagonal principal;

• Alterar linha da matriz dos coeficientes;

• Alterar linha do vetor das constantes.

Escalonamento com pivoteamento

• Repetir da primeira até a penúltima coluna;

• Verificar a necessidade de se fazer o pivoteamento;

• Procurar uma linha adequada;

• No caso de encontrar, fazer a permuta das linhas;

• Verificar a necessidade de se fazer o escalonamento da coluna corrente;

• Repetir para as linhas abaixo da diagonal principal;

• Aplicar operação elementar com o objetivo de zerar o elemento da linha corrente abaixo da diagonal principal;

• Alterar linha da matriz dos coeficientes;

• Alterar linha do vetor das constantes.

Fonte: http://www1.univap.br/spilling/CN/apostila1.pdf

Fonte: RUGGIERO, M. A. G. e LOPES, V. L. .R. CÁLCULO NUMÉRICO: Aspectos teóricos e computacionais; 2ª edição. Cap. 3, P 119 – 125.

Método de decomposição A = LU

O método da fatoração A = LU é uma outra ferramenta da solução direta de sistemas lineares da forma Ax = b. É de certa utilidade para sistemas em que a sua matriz pode ser fatorada em outras duas, ou seja, A = LU, em que L é uma matriz triangular inferior, possui valores não nulos abaixo e na diagonal, e U é matriz triangular superior, os valores não nulos são acima e na diagonal.

Procedimento para se achar as matrizes triangulares de uma matriz original A:

Assumir que a eliminação de Gauss pode ser realizada no sistema linear Ax = b, sem que haja trocas de linha.
Multiplicar a matriz A original pela matriz de transformação de Gauss M(k), em que k = 1, 2, 3,..., n-1, e repetir esse processo até que se chegue a uma matriz triangular superior.

A matriz de transformação é formada por uma diagonal principal composta por 1, e para um dado k, por elementos negativos -mk+1, k até -mn, k, que possuem valores e são calculados através da equação mj, 1 = a(1)j1 / a(1)11, em que a(1)j1 é o elemento da j-ésima linha e a(1)11 é o primeiro elemento da matriz original.

Achar a inversa da matriz de transformação de Gauss, [M(k)]-1, em que k = 1, 2, 3,..., n. Esse procedimento fornece os valores das colunas da matriz triangulo inferior, L(k).
Multiplicar todas as matrizes L(k), para k = 1, 2, 3,..., n. Isso resultará na matriz triangular inferior L.

Resolução de um sistema linear:

Utilizar o processo de substituição regressiva para se encontrar o sistema na forma triangular.
Converter os sistemas para matriz A e matriz superior.
Através do passo 3 do procedimento de encontrar matrizes triangulares, encontrar a matriz triangular inferior.
Substituir A por LU, na equação Ax = b (1).
Substituir Ux por y, um vetor cujos valores são y(i), em que i = 1, 2, 3,..., n, na equação (1), chegando a Ly = b (2).
Resolver a equação Ux = y, usando os valores obtidos no passo anterior. A partir dessa equação, se chega aos valores das incógnitas do vetor x.

Apesar de ser um método trabalhoso, é útil para reduzir o número de operações necessárias para se resolver um sistema linear. Quando trabalhamos com um sistema linear do tipo Ax = b usando o método de eliminação de Gauss, são necessárias O(n3/3) operações, enquanto sistemas lineares que envolvam sistema triangulo superior, que utilizam substituição regressiva, necessitam de O(n²) operações.

Resumindo: