3. Descreva, fazendo um passo-a-passo explicativo (pode conter um pseudocódigo, fluxograma, etc), como resolver sistemas de equações lineares usando os métodos iterativos: (i) Jacobi e (ii) Gauss-Seidel.
Método de Jacobi
O método de Jacobi é um algoritmo para resolver sistemas de equações lineares, tem o nome do matemático Alemão Carl Gustav Jakob Jacobi. Como o exemplificado abaixo:
Dada uma matriz quadrada de 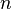 equações lineares:
equações lineares:  em que:
em que:
Então A pode ser decomposto num componente diagonal D e o resto R:
O sistema de equações lineares pode ser reescrito como:
O método de Jacobi é um método iterativo que resolve o membro esquerdo da expressão em ordem a x ao usar o método resultante da iteração anterior no membro direito. Analiticamente, isto pode ser escrito como:
Fluxograma
Exemplo:
Método de Gauss-Seidel
O método de Gauss-Seidel é um método iterativo para resolução de sistemas de equações lineares, seu nome é uma homenagem aos matemáticos alemães Carl Friedrich Gauss e Philipp Ludwig von Seidel. É semelhante ao método de Jacobi (e como tal, obedece ao mesmo critério de convergência). É condição suficiente de convergência que a matriz seja estritamente diagonal dominante, i. e., fica garantida a convergência da sucessão de valores gerados para a solução exata do sistema linear.
Procuramos a solução do conjunto de equações lineares, expressadas em termos de matriz como:
A iteração Gauss-Seidel é
onde  ; as matrizes
; as matrizes  ,
,  , e
, e  representam respectivamente os coeficientes da matriz
representam respectivamente os coeficientes da matriz  : a diagonal, triangular estritamente inferior, e triangular estritamente superior; e
: a diagonal, triangular estritamente inferior, e triangular estritamente superior; e 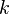 é o contador da iteração. Esta expressão matricial é utilizada principalmente para analisar o método. Quando implementada, Gauss-Seidel, uma aproximação explícita de entrada por entrada é utilizada:
é o contador da iteração. Esta expressão matricial é utilizada principalmente para analisar o método. Quando implementada, Gauss-Seidel, uma aproximação explícita de entrada por entrada é utilizada:
Diferenciando-se do método de Gauss-Jacob:
Sendo que o método de Gauss-Seidel apresenta convergência mais rápida que este último.
Note que o cálculo de 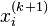 utiliza apenas os elementos de
utiliza apenas os elementos de  que já havia sido calculada e apenas aqueles elementos de
que já havia sido calculada e apenas aqueles elementos de 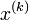 já haviam avançado para a iteração
já haviam avançado para a iteração 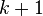 . Isto significa que nenhum armazenamento adicional é necessário, e que computacionalmente pode ser substituído (
. Isto significa que nenhum armazenamento adicional é necessário, e que computacionalmente pode ser substituído (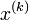 por
por  ). A iteração geralmente continua até que a solução esteja dentro da tolerância especificada.
). A iteração geralmente continua até que a solução esteja dentro da tolerância especificada.
Calculando o Erro
O cálculo do erro consiste em se pegar a maior diferença entre as raízes da iteração k-1 e k, e dividi-las por o valor de x máximo da iteração atual;
Diferença entre os dois métodos
Nota-se que a computação de  , no método de Jacobi é feita com base em todos os valores obtidos em iterações anteriores. Ao contrário do método de Gauss-Seidel, não se pode reescrever
, no método de Jacobi é feita com base em todos os valores obtidos em iterações anteriores. Ao contrário do método de Gauss-Seidel, não se pode reescrever 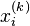 com
com 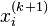 , pois esse valor é necessário durante a continuação da computação. Esta é a diferença mais significativa entre o método de Jacobi e o método de Gauss-Seidel e é o motivo que o torna um algoritmo paralelo.
, pois esse valor é necessário durante a continuação da computação. Esta é a diferença mais significativa entre o método de Jacobi e o método de Gauss-Seidel e é o motivo que o torna um algoritmo paralelo.
Diagrama mostrando esquematicamente a dependência de cada um dos termos nas três primeiras iterações de uma matriz A:3x3 dos métodos de Gauss-Jacobi e Gauss-Seidel.
Referências
RUGGIERO, M. A. G. e LOPES, V. L. .R. CÁLCULO NUMÉRICO: Aspectos teóricos e computacionais; 2ª edição. Cap. 3, p. 155 - 176.
4. Analisar a convergência usando o critério das linhas e o critério de Sassenfeld do seguinte sistema linear e resolvê-lo usando os dois métodos iterativos explicados no exercício anterior. Usar x0 = (-2,4; 5; 0; 3) e tolerância ε<10-2
5x1 + 2x2 + x3 = 7,
-x1 + 4x2 + 2x3 = 3,
2x1 - 3x2 + 10x3 = -1.
Convergência: Critério das Linhas
Este método pode também ser aplicado para análise de convergência no método de Seidel.
Resolução pelo método de Jacobi (Excel)
X2=0,9971
X3=-0,0008
Resolução pelo método de Gauss-Seidel (Scilab)
A função resulta em 6 interações e seus valores finais são: 1.000068869335937 ; 1.000212232470703 e 0.000049895874023.
Podemos observar que há uma diferença no número total de interações necessárias entre os métodos de Jacobi e Gauss-Seidel, de 10 para 6 interações; nesse sistema em específico, o segundo método mostra-se mais eficiente uma vez que haja uma diminuição de 40% nas interações em relação ao primeiro.
5. [OPCIONAL] Resolva o seguinte sistema linear usando o metodo de Jacobi.
Usar x0 = (0,7 ;-1,6 ;0,6) e tolerância < 10-2.
10x1 + 2x2 + x3 = 7 ;
x1 + 5x2 + x3 = -8 ;
2x1 + 3x2 + 10x3 = 6 :
Solução exata e x1 = 1; x2 = -2 e x3 = 1