Erro da fórmula simples da regra de Simpson
Formula composta da regra de Simpson
Para obter a fórmula composta da primeira Regra de Simpson, deve-se dividir o intervalo [a,b] em n subintervalos de espaçamento h=(b-a)/n e aplicar a casa par de subintervalos [xi-1, xi], [xi, xi+1] para todo i = 1, 2, …, n-1, a fórmula simples da primeira Regra de Simpson.
Desta forma, obtém-se:
sendo n um número par.
Erro da fórmula composta
Fonte: http://www.decom.ufop.br/marcone/Disciplinas/MetodosNumericoseEstatisticos/Integracao.pdf
R: Assim o número mínimo de subintervalos é 16
→ Regra do Trapézio:
Fazendo h = (x1 – x0)/n, onde nesse caso n = 1 (n é o número de subdivisões do intervalo [x1, x0]) e substituindo os fatores de Lagrange no polinômio.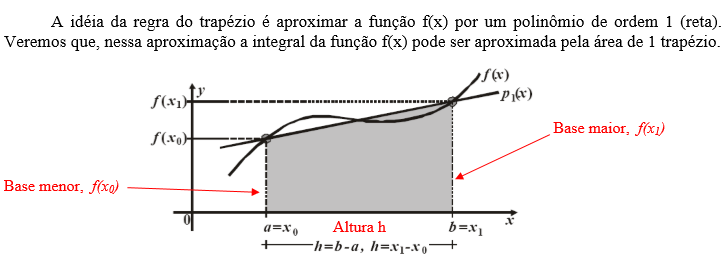
→ Para realização desses cálculos foi empregado o software Excel:
Pela tabela 1:
IT = ((B7 – B3) / 2) * (C3 + C7)
IT = ((2,6 - 1,8) / 2) * (3,12014 + 10,46675)
IT = 5,434756
→ Erro associado a Regra do Trapézio:
Abaixo temos o gráfico de f(x) com a linha de tendência (exponencial) e sua equação, que representa uma aproximação de f(x), visto que a equação não foi fornecida explicitamente. Pra construção deste gráfico foram empregados os dados da tabela 1, que são fornecidos no enunciado do exercício.
Como o cálculo do erro da Regra do Trapézio, envolve a segunda derivada da função obtida através da tabela (d^2/dx^2 (0,1745714683 * exp(1,5407882266 * x)), o software Wolfram Alpha foi utilizado para obtê-la:
ET = (POTÊNCIA((B7 – B3);3) / 12) * (0,510537586426463 * EXP(0,2) * (1,5407882266 * C7))
ET = ((2,6 – 1,8)^3 / 12) * (0,510537586426463 * EXP(0,2) * (1,5407882266 * 10,46675))
ET = 0,42907196
→ Regra do Trapézio repetida:
ITR = (((B7 – B3) / 4) / 2) * (C3 + C7 + 2 * (C4 + C5 + C6))
ITR = ((2,6 – 1,8) / 2) * (3,12014 + 10,46675 + 2 *(3,12014 + 6,04241 + 6,04241))
ITR = 4,399681
→ Erro associado a Regra do Trapézio repetida:
ETR = (POTÊNCIA(((B7 – B3) / 4); 3) / 12 * POTÊNCIA(4; 2)) * (0,510537586426463 * EXP(0,2) * (1,5407882266 * C7))
ETR = (((2,6 – 1,8)/4)^3 / 12 * (4^2)) * (0,510537586426463 * EXP(0,2) * (1,5407882266 * 10,46675))
ETR = 0,10726799
→ Discussão:
A diferença entre IT – ITR = 5,434756 – 4,399681 é 1,035075;
A diferença entre ET – ETR = 0,42907196 – 0,10726799 é 0,32180397;
Tais resultados demonstram, como era esperado, que a Regra do Trapézio repetida é mais precisa do que sua forma “simples”. No que se refere ao valor da aproximação da integral, compreende-se que a maior precisão na Regra do trapézio repetida se deve ao uso de todos os valores que dividem a função nos 4 intervalos.
Já ao valor do erro, foi obtido de forma aproximada, através da linha de tendência da função descrita pela tabela, compreende-se que poderia haver maior precisão, contudo ao tentarmos realizar a Interpolação da função pela forma de Lagrange, percebe-se que tais cálculos chegariam em uma função de elevados expoente e complicada resolução, portanto, optamos por aproximar a função através da linha de tendência, traçada no gráfico acima, com o Excel empregando os dados da tabela.
Percebe-se que a precisão é maior na forma repetida devido ao termo n² aplicado no denominador, intui-se que este foi empregado, pois ele aparece duas vezes implicitamente na forma repetida da Regra do Trapézio aplicada a função, sendo a primeira na composição do termo h = (b – a) / n e a segunda no somatório dos pontos descritos f(xi), uma vez que o intervalo entre os pontos é o valor de n.
→ Regra 1/3 de Simpson:
Após as operações, necessárias, é possível chegar a fórmula: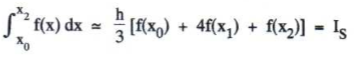
Is = =(((B8 – B4) / 2) / 3) * (C4 + 4 * ((B8 + B4) / 2) + C8)
Is = (((2,6 – 1,8) / 2) / 3)*(3,12014 + 4 * ((1,8 + 2,6) / 2)+ 10,46675)
Is = 2,984918667
→ Erro associado a fórmula de 1/3 de Simpson:
Como o cálculo do erro 1/3 de Simpson, envolve a segunda derivada da função obtida através da tabela (d^4/dx^4 (0,1745714683 * exp(1,5407882266 * x)), o software Wolfram Alpha foi utilizado para obtê-la:
Es = ((POTÊNCIA((B8 – B4); 5) / 2880) * (0,149307690249953 * EXP(0,4) * (1,5407882266 * C8)))
Es = ((POTÊNCIA((2,6 – 1,8); 5) / 2880) * (0,149307690249953 * EXP(0,4) * (1,5407882266 * 10,46675)))
Es = 0,00408707
→ Regra 1/3 de Simpson repetida:
→ Erro associado a fórmula de 1/3 de Simpson repetida:
Esr = ((POTÊNCIA((B8 – B4); 5) / 2880 * POTÊNCIA((4 / 2); 4))) * (0,149307690249953 * EXP(0,4) * (1,5407882266 * C8))
Esr = ((POTÊNCIA((2,6 – 1,8); 5) / 2880 * POTÊNCIA((4 / 2); 4))) * (0,149307690249953 * EXP(0,4) * (1,5407882266 * 10,46675))
Esr = 0,006539314
→ Discussão:
A diferença entre Is – Isr = 2,984918667 – 4,154794 é -1,169875333;
A diferença entre Es – Esr = 0,00408707 – 0,006539314 é -0,006130607;
Tais resultados demonstram, como era esperado, que a Regra 1/3 de Simpson repetida é mais precisa do que sua forma “simples”, uma vez que tem valores mais próximos da Regra do Trapézio Repetida. No que se refere ao valor da aproximação da integral, compreende-se que a maior precisão na Regra 1/3 de Simpson repetida se deve ao uso de todos os valores que dividem a função nos 4 intervalos.
Da mesma maneira que na regra do Trapézio, optou-se por aproximar a função através da linha de tendência, traçada no gráfico acima, com o Excel empregando os dados da tabela, para que se pudesse calcular um a aproximação par o erro associado.
Da mesma forma que na Regra do Trapézio Repetida, percebe-se que a precisão é maior na forma repetida da regra 1/3 de Simpson, devido ao termo n² aplicado no denominador.
Como era esperado as formas repetidas das duas regras tem mair precisão e se assemelham muito em valores, tendo em vista que o valor da integral na regra do Trapézio Repetida foi de 4.399681, já na Regra 1/3 de Simpson Repetida foi de 4.154794, com erros de 0,10726799 e 0,006539314, respectivamente. Como o erro da regra de Simpson é menor, podemos supor que ela é mais precisa.
→ Referências:
1 RUGGIERO, M. A. G. e LOPES, V. L. R. CÁLCULO NUMÉRICO: Aspectos teóricos e computacionais; 2ª edição. Cap. 7, p. 295 – 310.
2 http://www1.univap.br/spilling/CN/CN_Capt6.pdf
Como os valores fornecidos neste exercício, representam os Erros dos valores encontrados no exercício 4 de f(x), podemos descobrir qual o erro relacionado aos diferentes métodos, basta somar o valor de f(x) do Exercício anterior com o erro associado a f(x), e dessa maneira, verificar a diferença entre os cálculos.
No caso do método dos trapézios, a formula utilizada foi:
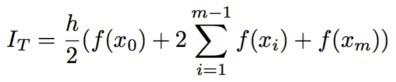
No caso do método dos trapézios, a formula utilizada foi:
portanto, onde estão as funções, somaremos o erro associado a cada ponto, tornando a equação da seguinte forma:
E o resultado da equação com o erro associado foi de: 4,39968064.
O resultado dessa equação sem os erros associados, calculado no exercício 4, é de 4,399681. O erro do método dos trapézios portanto é de: 0.00000036
Agora pelo método de Simpson, mantemos a equação usada no ex 4:
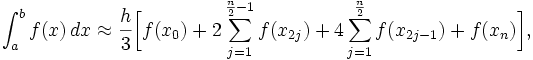
substituímos os valores o que resultou na seguinte equação:
substituímos os valores o que resultou na seguinte equação:
O resultado da equação foi de: 4,154793373.
No método de Simpson sem considerar os erros, chegamos no resultado de 4,154794.
O erro desse método é 0.0000006267.
Logo o erro de ambos os métodos é pequeno, isso acontece porque o erro associado a f(x) é um erro muito pequeno, na ordem de 0.0000006.